What is Standard Deviation
Change and Standard deviation are the two significant subjects in Measurements. It is the proportion of the scattering of factual information. Scattering is the degree to which values in a circulation vary from the normal of the conveyance. To evaluate the degree of the variety, there are particular measures to be specific:
(I) Reach
(ii) Quartile Deviation
(iii) Mean Deviation
(iv) Standard Deviation
The level of scattering determined by the system of estimating the variety of important pieces of information. In this article, you will realize what is change and standard deviation, recipes, and the method to track down the qualities with models
What are the Variance and Standard Deviation?
In measurements, Difference and standard deviation connected with one another since the square base of fluctuation viewed as the standard deviation for the given informational index. The following are the meanings of fluctuation and standard deviation.
What is difference?
Fluctuation is the proportion of how strikingly an assortment of information fanned out. On the off chance that every one of the information values are indistinguishable, it demonstrates the fluctuation is zero. All non-zero fluctuations are viewed as certain. A little change addresses that the information focuses are near the mean, and to one another, though on the off chance that the information focuses are exceptionally fanned out from the mean and from each other demonstrates the high fluctuation. To put it plainly, the fluctuation is characterized as the normal of the squared separation from each highlight the mean.
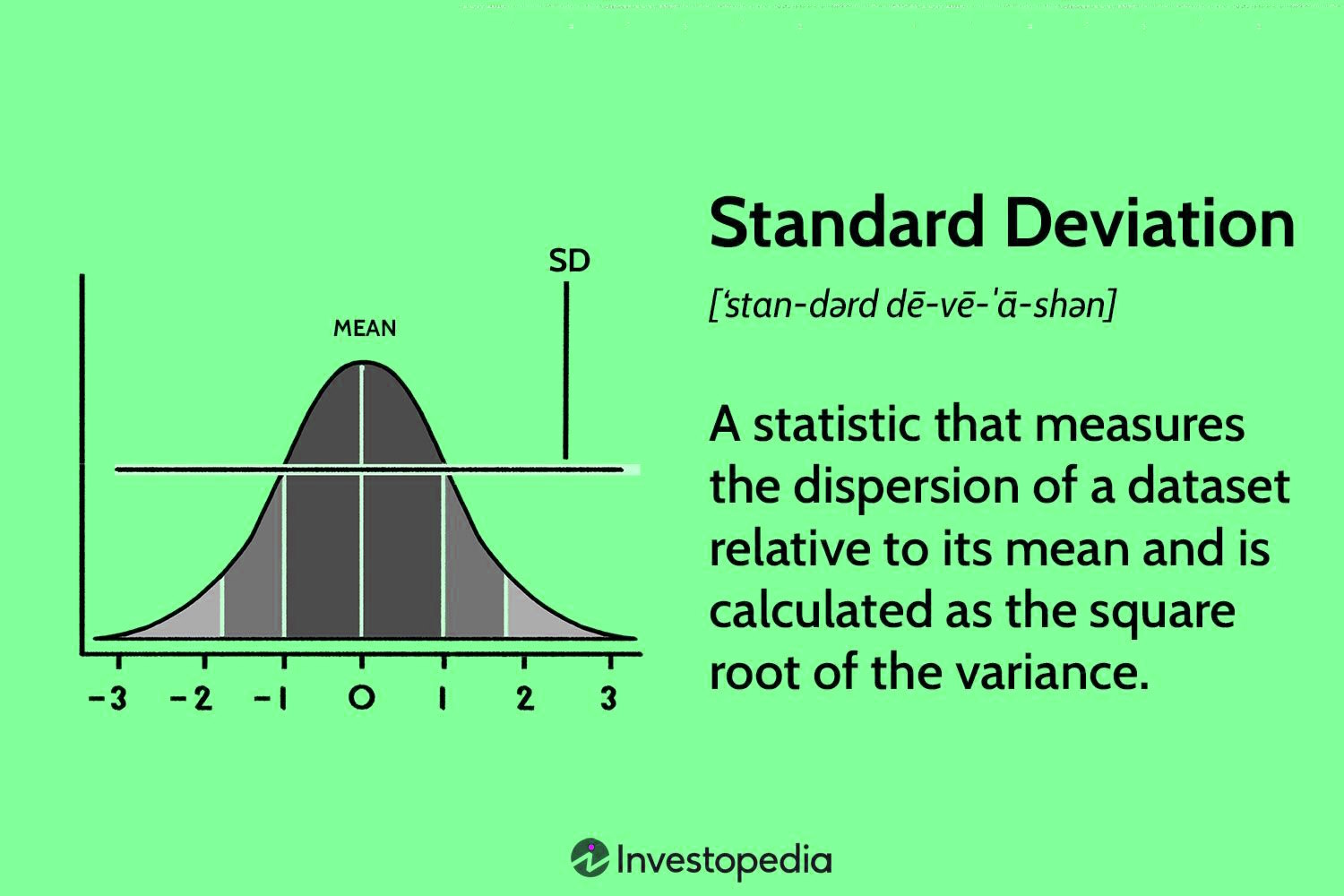
Standard Deviation is an action which shows how much variety (like spread, scattering, spread,) from the mean exists. It shows a “regular” deviation from the mean. It is a famous proportion of changeability since it gets back to the first units of proportion of the informational index. Like the fluctuation, in the event that the information focuses are near the mean, there is a little variety though the information focuses are exceptionally fanned out from the mean, then it has a high difference. Standard deviation computes the degree to which the qualities vary from the normal. It also, the most generally utilized proportion of scattering, depends on all qualities. In this way an adjustment of even one worth influences the worth of standard deviation. It is autonomous of beginning however not of scale. It is additionally valuable in specific high level factual issues.
How calculated?
The equation for standard deviation utilizes three factors. The principal variable is the worth of each point inside an informational index, with a total number demonstrating each extra factor (x, x1, x2, x3, and so on). The mean is applied to the upsides of the variable M and the quantity of information that is relegated to the variable n. Change is the normal of the upsides of squared contrasts from the number-crunching mean.
To compute the mean worth, the upsides of the information components added together and the complete separated the quantity of information elements that involved.
Standard deviation, signified the image σ, portrays the square base of the mean of the squares of the multitude of upsides of a series got from the number juggling mean which likewise called the root-mean-square deviation. 0 is the littlest worth of standard deviation since it can’t be negative. At the point when the components in a series are more confined from the mean, then, at that point, the standard deviation is likewise enormous.
The factual apparatus of standard deviation is the proportions of scattering that figures the inconsistency of the scattering among the information. For example, mean, middle and mode are the proportions of focal inclination. Hence, these viewed as the focal first request midpoints. The proportions of scattering that referenced straight over are midpoints of deviations that outcome from the typical qualities, hence these called second-request midpoints.
Standard Deviation Example
We should work out the standard deviation for the quantity of gold coins on a boat run by privateers.
There are a sum of 100 privateers on the boat. Genuinely, it implies that the populace is 100. We utilize the standard deviation condition for the whole populace on the off chance that we know various gold coins each privateer has.
Genuinely, we should consider an example of 5 and here you can involve the standard deviation condition for this example populace.
This implies we have an example size of 5 and for this situation, we utilize the standard deviation condition for the example of a populace.
Standard deviation of Grouped Data
In the event of gathered information or assembled recurrence dissemination, the standard deviation can found by considering the recurrence of information values. This can perceived with the assistance of a model.
Frequently Asked Questions – FAQs
Q1
How would you work out the standard deviation?
The technique to compute the standard deviation is given underneath:
Stage 1: Register the mean for the given informational index.
phase 2: Take away the mean from every perception and compute the square in each example.
Stage 3: Track down the mean of those squared deviations.
Stage 4: At long last, take the square root got mean to get the standard deviation.
Q2
What does Standard Deviation tell you?
Standard deviation lets us know how far is the mean from every perception in the given informational index. As such, it shows the regular deviation from the mean.
Q3
What is the standard deviation and change?
Standard deviation demonstrates how the spread of perceptions of an informational collection is from the mean by learning at the change’s square root. The fluctuation appraises the typical degree to which every perception varies from the mean of all perceptions of the information.
Q4
What is the standard deviation model?
Consider the informational index: 2, 1, 3, 2, 4. The mean and the amount of squares of deviations of the perceptions from the mean will be 2.4 and 5.2, separately. Consequently, the standard deviation will be √(5.2/5) = 1.01.
Q5
For what reason do we utilize standard deviation?
A standard deviation is utilized to decide how assessments for a gathering of perceptions (i.e., informational collection) are fanned out from the mean (normal or anticipated esteem).

How It Works
Standard deviation is a factual estimation that is in many cases utilized in finance, especially in money management. When applied to the yearly pace of return of a venture, it can give data on that speculation’s authentic instability. This implies that it shows how much the cost of that venture has changed over the long run.
The more prominent the standard deviation of protections, the more noteworthy the change between each cost and the mean, which shows a bigger cost range. For instance, an unpredictable stock has an exclusive expectation deviation, implying that its cost goes all over much of the time. The standard deviation of a steady blue-chip stock, then again, is generally rather low, implying that its cost is typically steady.
Standard deviation can likewise be utilized to anticipate execution patterns. In effective financial planning, for instance, a record store is intended to repeat a benchmark file. This implies that the asset will have a low standard deviation from the worth of the benchmark.
Then again, forceful development reserves frequently have an elevated expectation deviation from relative stock files. This is on the grounds that their portfolio chiefs make forceful wagers to create higher-than-normal returns. This better quality deviation connects with the degree of chance financial backers can anticipate from that record.
Standard deviation is one of the key principal risk estimates that examiners, portfolio chiefs, and counselors use. Trading companies report the standard deviation of their shared assets and different items. An enormous scattering shows how much the profit from the asset is straying from the normal typical returns. Since it is straightforward, this measurement is routinely answered to the end clients and financial backers.
Calculating Standard Deviation
Standard deviation is determined as keeps:
Ascertain the mean of all data of interest. The mean is determined by adding every one of the useful pieces of information and separating them by the quantity of data of interest.
Ascertain the difference for every data of interest. The change for every information point is determined by taking away the mean from the worth of the data of interest.
Square the difference of every piece of information (from Stage 2).
Amount of squared fluctuation values (from Stage 3).
Partition the amount of squared change values (from Stage 4) by the quantity of data of interest in the informational collection less 1.
Take the square foundation of the remainder (from Stage 5).
Key Properties of Standard Deviation
One critical property of standard deviation is additivity. This implies that the standard deviation of an amount of irregular factors. This implies that investigators or specialists utilizing standard deviation are looking at numerous significant pieces of information, as opposed to making determinations in light of just breaking down single marks of information, which prompts a more serious level of precision.
One more property of standard deviation is scale invariance. This is especially valuable in contrasting the changeability of datasets and various units of estimation. For instance, if one dataset is estimated in inches and one more in centimeters, their standard deviations can in any case measure up straightforwardly without expecting to change over units.
Last, standard deviation has properties of evenness and non-antagonism. This implies a standard deviation is dependably certain and evenly conveyed around the mean. This evenness property suggests that deviations over the mean are adjusted by deviations beneath the mean, bringing about an all out equilibrium of the whole informational index. The property of continuously being positive means a it has a more serious level of equivalence while taking a gander at this across informational collections.
Standard Deviation vs. Variance
Change and standard deviation are connected measurements. Change is inferred by taking the mean of the pieces of information, deducting the mean from every information point separately, squaring every one of these outcomes, and afterward taking one more mean of these squares. Standard deviation is the square base of the change.
Change decides the information’s spread size when contrasted with the mean worth. As the difference gets greater, more variety in information values happens, and there might be a bigger hole between one information esteem and another. On the off chance that the information values are near one another, the fluctuation will be more modest. In any case, this is more hard to get a handle on than the standard deviation since changes address a squared outcome that may not be genuinely communicated on a similar diagram as the first dataset.
Standard deviations are generally simpler to picture and apply. The standard deviation communicated in similar unit of estimation as the information, which isn’t really the situation with the change. Utilizing the standard deviation, analysts might decide whether the information has a typical bend or other numerical relationship.
On the off chance that the information acts in a typical bend, 68% of the information focuses will fall inside one standard deviation of the normal, or mean, data of interest. Bigger changes cause more information focuses to fall outside the standard deviation. More modest differences bring about additional information that is near normal.
How Standard Deviation Is Used in Business
Standard deviation isn’t just utilized in effective money management. Business examiners or organizations can involve standard deviation in various ways of surveying risk, make expectations, and oversee organization activities.
Risk The board
Standard deviation is broadly utilized in business for risk the executives. It helps organizations measure and oversee different kinds of dangers. By ascertaining the standard deviation of specific results, organizations can evaluate the unpredictability or vulnerability related with how they works. For instance, an organization can utilize standard deviation to gauge the gamble of various items being returned.
Monetary Examination
In money and bookkeeping, standard deviation is utilized to break down monetary information and evaluate the fluctuation of monetary execution measurements. For instance, standard deviation is utilized to gauge the instability of venture returns. This can used to decide risk-return tradeoffs and the procedure of how an organization needs to send capital.
Anticipating
Standard deviation is utilized in deals anticipating to evaluate the fluctuation of deals information and foresee future deals patterns. Standard deviation assists organizations with recognizing irregularity, patterns, and examples in deals information that permit them to make arrangements for cash needs soon.
Quality Control
In assembling and activities the executives, standard deviation is utilized to screen and further develop item quality. Standard deviation is likewise utilized in quality control cycles, for example, Six Sigma procedures to quantify process ability, diminish absconds, and streamline producing processes for worked on quality and consumer loyalty.
Project The board
Standard deviation is utilized in project the board to evaluate project execution and oversee gambles. For instance, standard deviation can be utilized connected with basic way investigation and acquired esteem. It can used to measure fluctuations, track progress, and evaluate risk connected with a basic way or procured esteem not being accomplished.
Qualities and Limits of Standard Deviation
Like any factual estimation for breaking down information, standard deviation has the two qualities and restrictions that ought to be considered before it is utilized.
Strengths
- Commonly used
- Includes all data points
- Can combine datasets
- Further computational uses
Limitations
- Doesn’t measure dispersion
- Impact of outliers
- Difficult to calculate manually
Qualities
Normally utilized:It is a generally utilized proportion of scattering. Numerous experts are presumably more acquainted with this than contrasted with other measurable computations of information deviation. Hence,It is utilized by different callings, from financial backers to statisticians.
Incorporates all data of interest: It is comprehensive of perceptions. Every information point is remembered for the examination. Different estimations of deviation, for example, range just measure the most scattered focuses without thought for the in the middle between. Hence,it is much of the time considered a more powerful, precise estimation contrasted with different perceptions.
Can join datasets: The standard deviation of two informational collections can be consolidated utilizing a particular consolidated its equation. There are no comparable equations for other scattering perception estimations in measurements.
Further computational purposes: Dissimilar to different method for perception,it can be utilized in additional logarithmic calculations, importance there’s a flexibility to standard deviation.
Restrictions
Doesn’t quantify scattering: The standard deviation doesn’t really gauge how far an information point is from the mean. All things considered, it looks at the square of the distinctions, an unpretentious however eminent contrast from genuine scattering from the mean.
Effect of exceptions: Anomalies heavierly affect it. This is particularly obvious considering the distinction from the mean is squared, bringing about a much bigger amount contrasted with different data of interest. In this manner, be careful that standard perception normally gives more weight to outrageous qualities.
Challenging to estimations work out physically: rather than different estimations of scattering like reach (the most elevated esteem short the least worth), It requires a few bulky advances and is bound to cause computational mistakes contrasted with simpler. This obstacle can be circumnavigated using a Bloomberg terminal.
What Does an Exclusive requirement Deviation Mean?
An enormous standard deviation demonstrates that there is a ton of difference in the noticed information around the mean. This demonstrates that the information noticed is very fanned out. A little or low would show rather that a large part of the information noticed is bunched firmly around the mean.
What Does Standard Deviation Tell You?
Standard deviation depicts how scattered a bunch of information is. It looks at every information highlight the mean of all data of interest, and it returns a determined worth that portrays whether the information focuses are in closeness or whether they are fanned out. In an ordinary dissemination, so. lets you know how far values are from the mean.
How Would You Track down Rapidly?
Assuming that you take a gander at the dissemination of a few noticed information outwardly, you can check whether the shape is somewhat thin versus fat. Fatter conveyances have greater standard deviations. On the other hand, Succeed has inherent standard deviation capabilities relying upon the informational collection.
A lower standard deviation isn’t be guaranteed to better. It demonstrates more gamble, which financial backers could possibly like. While evaluating how much deviation in their portfolios, financial backers ought to think about their capacity to bear unpredictability and their general speculation goals. More forceful financial backers might be alright with a speculation system that settles on vehicles with higher-than-normal unpredictability, while additional moderate financial backers may not.
The Primary concern it is a method for evaluating risk, particularly in business and financial planning. It involves the distance of focuses in a dataset from the mean of that dataset to find how scattered the set is, and consequently, how unstable it will in general be after some time.
Financial backers can utilize standard deviation to decide how steady or unsurprising a speculation is probably going to be. Organizations utilize it or survey risk, oversee tasks, and plan incomes. Like some other factual estimation, it has qualities and impediments, which ought to be considered when it is utilized.